Task-Driven Hybrid Model Reduction for Dexterous Manipulation
Wanxin Jin and Michael Posa
The GRASP Laboratory, University of Pennsylvania
 Code (Github)
Code (Github)
 Paper (Arxiv)
Paper (Arxiv)
Abstract: Many critical tasks in robotics, like dexterous manipulation, are inherently contact-rich; the hybrid nature of making and breaking contact creates significant challenges for model representation and control. Specifically, for a task like in-hand manipulation, the combinatoric complexity in representing and choosing potential contact locations and sequences between robot and object, where there are thousands of potential hybrid modes, is not generally tractable. In this paper, we are inspired by the key observation that far fewer modes are actually necessary to accomplish many tasks. Building on our prior work in learning hybrid models, represented as linear complementarity systems, we find a reduced-order hybrid model requiring only a limited number of task-relevant modes. This simplified representation, in combination with a model predictive controller, enables real-time control and is sufficient for achieving high performance on tasks like multi-finger dexterous manipulation. We show that reduced-order model learning with on-policy data provably bounds closed-loop performance, leading to a simple iterative method to improve the reduced-order model and controller. We demonstrate the proposed method first on synthetic hybrid systems, reducing the mode count by multiple orders of magnitude while achieving task performance loss of less than 5%. Second, in simulation environment, we apply the proposed method to solve three-finger robotic hand manipulation for object reorientation. With no prior knowledge, we achieve state-of-the-art closed-loop performance in less than five minutes of online learning.
Overview Video
Our Method
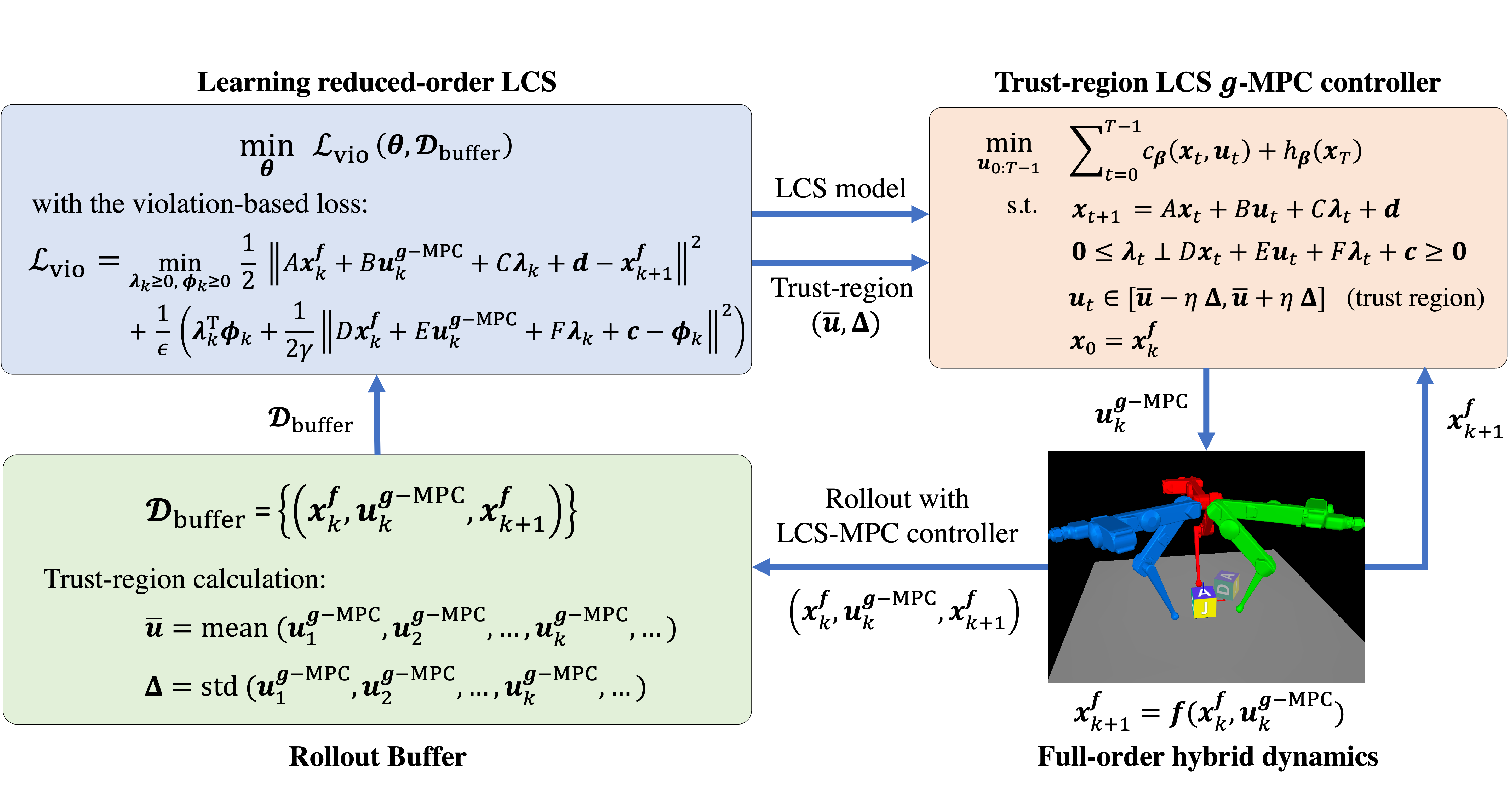
Fig. 1: Components of task-driven hybrid model reduction algorithm. There are three main components: learning reduced-order LCS, Trustregion LCS model predictive controller, and Rollout Buffer, each of which is detailed below.
Learning Reduced-Order Linear Complementarity System (LCS)
Linear Complementarity System (LCS), denoted as

is a compact representation of a piecewise affine system. Here, zero or non-zero of each entry of \(\boldsymbol{\lambda}\) determine the linear affine dynamics in each mode. The maximum number of potential modes is \(\color{red}2^{\dim \boldsymbol{\lambda}}\). For a reduced-order LCS, one can explicitly restrict the number of potential modes in LCS by setting \(\color{red}\dim \boldsymbol{\lambda}\).
The learning of a LCS i.e., identifying all matrices \((A,B,C,\boldsymbol{d},D,E,F,\boldsymbol{c})\), is based on our prior work
Trust-Region LCS-based Model Predictive Controller
We developed the LCS-based MPC controller, as part of our learning algorithm for on-policy data
collection and closed-loop control. The MPC controller is built on the direct method of trajectory optimization
Model Reduction on Synthetic Hybrid Control Systems
The task is to stabilize a piecewise affine (full-order) system, with a quadratic cost function. The full-order dynamics, denoted as \(\boldsymbol{f}()\), has more than 100 modes. The reduced-order LCS to be learned, denoted as \(\color{red}\boldsymbol{g}()\), has \(\color{red}\dim \boldsymbol{\lambda}=2\) (i.e., max. 4 modes). Below is the phase plot of the full-order dynamics \(\boldsymbol{f}\) with full-order MPC controller \(\boldsymbol{u}=\boldsymbol{f}\)-MPC\((\boldsymbol{x})\), versus with reduced-order MPC controller \(\boldsymbol{u}=\color{red}\boldsymbol{g}\)-MPC\((\boldsymbol{x})\). Different colors indicate different hybrid modes.
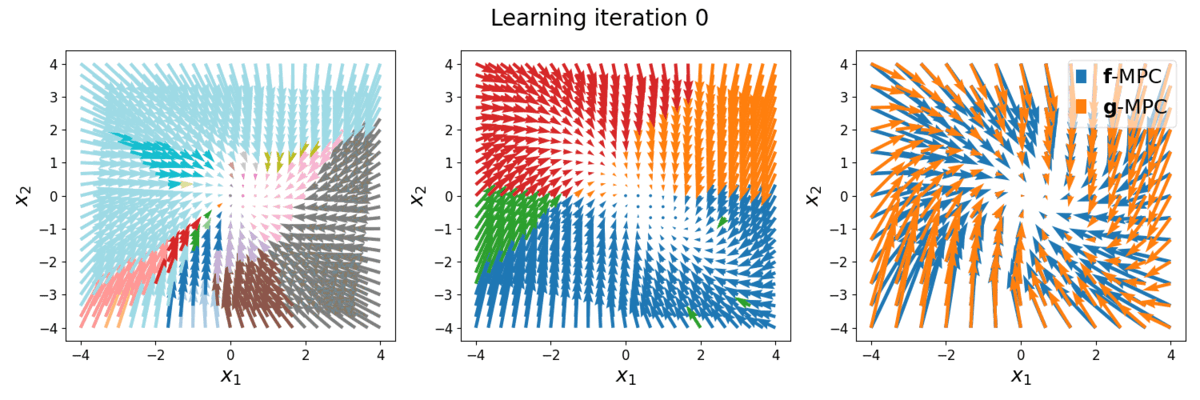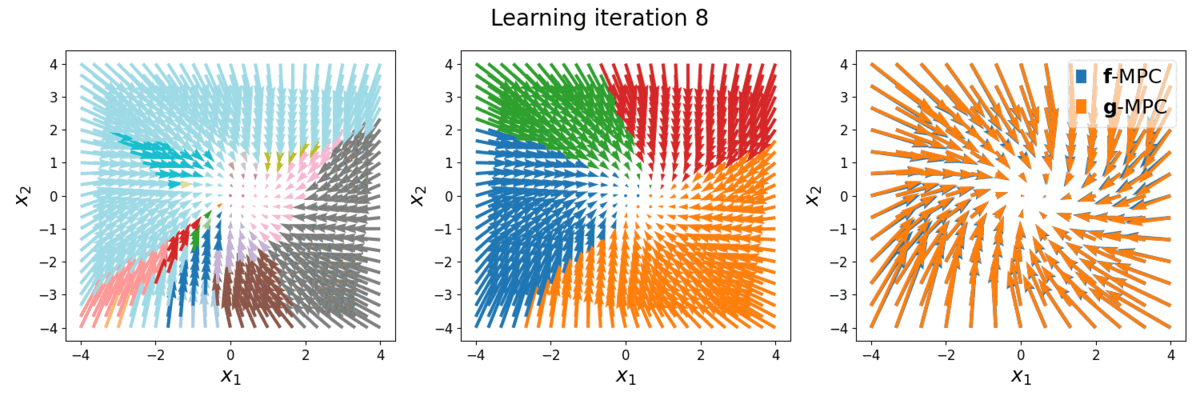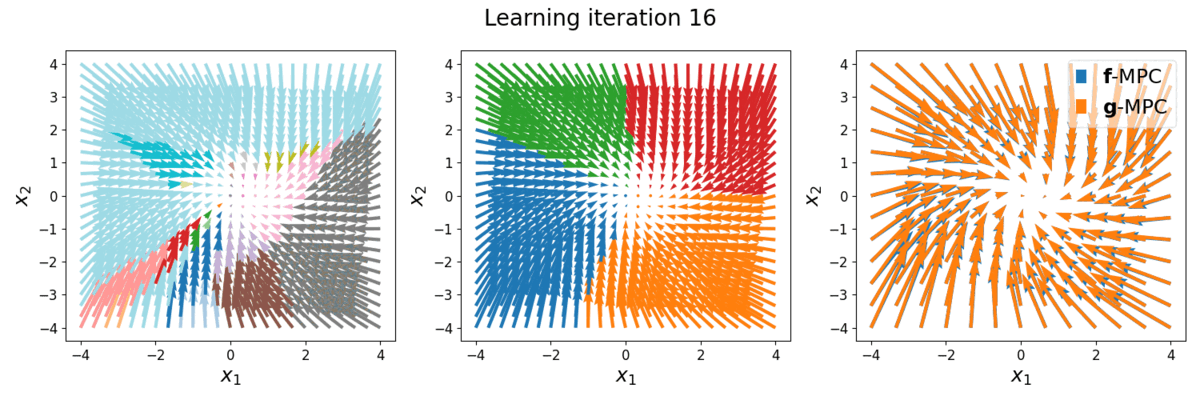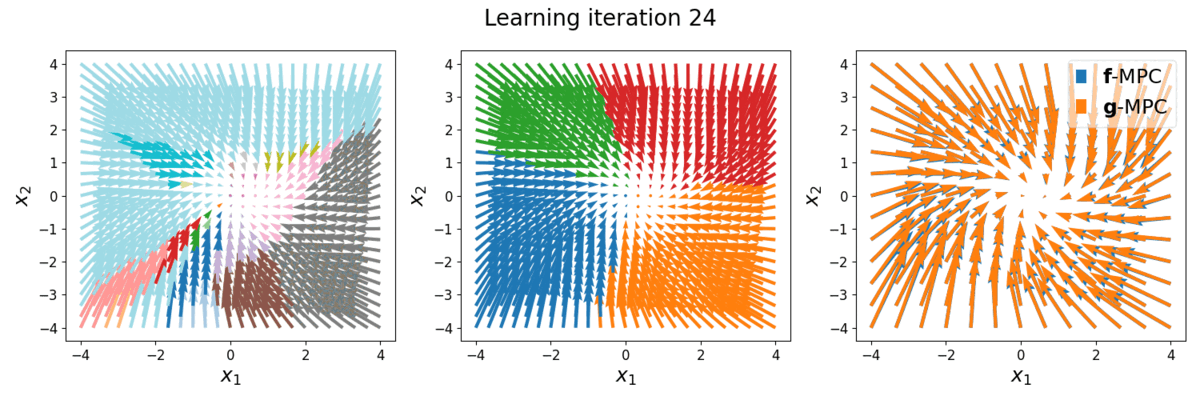
Left: phase plot of \(\boldsymbol{f}\) with full-order MPC controller, 43 modes (colors) are shown. Middle: phase plot of \(\boldsymbol{f}\) with reduced-order MPC controller at different learning iterations, 4 modes are shown. Right: Overlap comparison between the two phase plots.
The task is to stabilize a full-order LCS, with a quadratic cost function. The given full-order LCS, denoted as \(\boldsymbol{f}()\), has \(\dim \boldsymbol{\Lambda}=12\) (>1000 modes). The reduced-order LCS to be learned, denoted as \(\color{red}\boldsymbol{g}()\), has \(\color{red}\dim \boldsymbol{\lambda}=3\) (max. 8 modes). Below is the policy rollout on the full-order LCS \(\boldsymbol{f}\) with the full-order MPC controller, versus with the learned reduced-order MPC controller. Different colors indicate different hybrid modes.
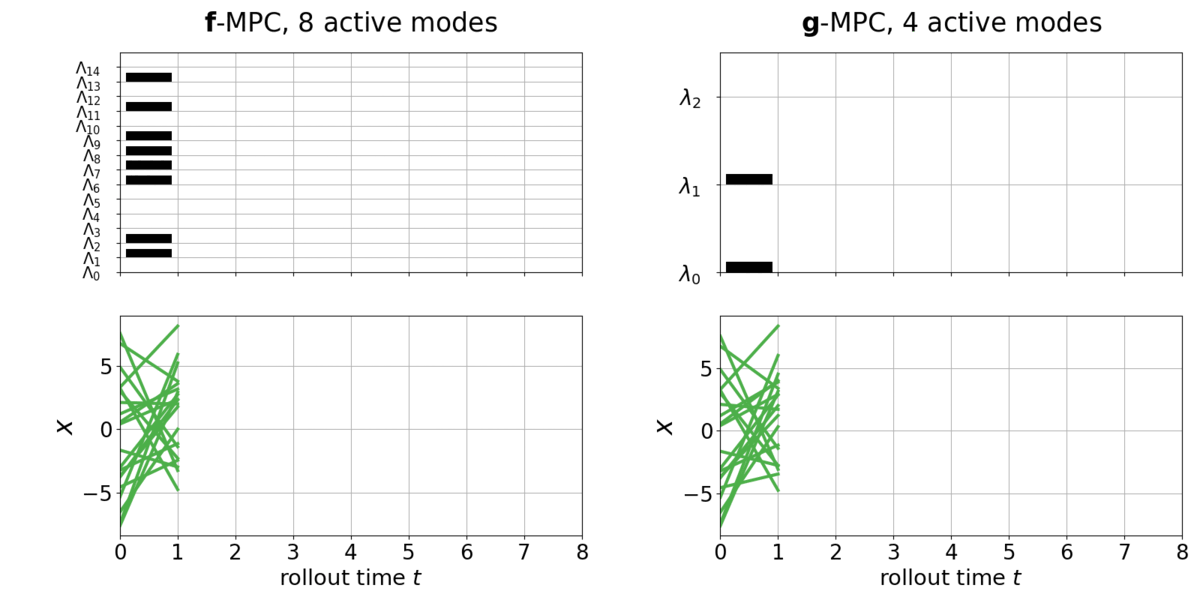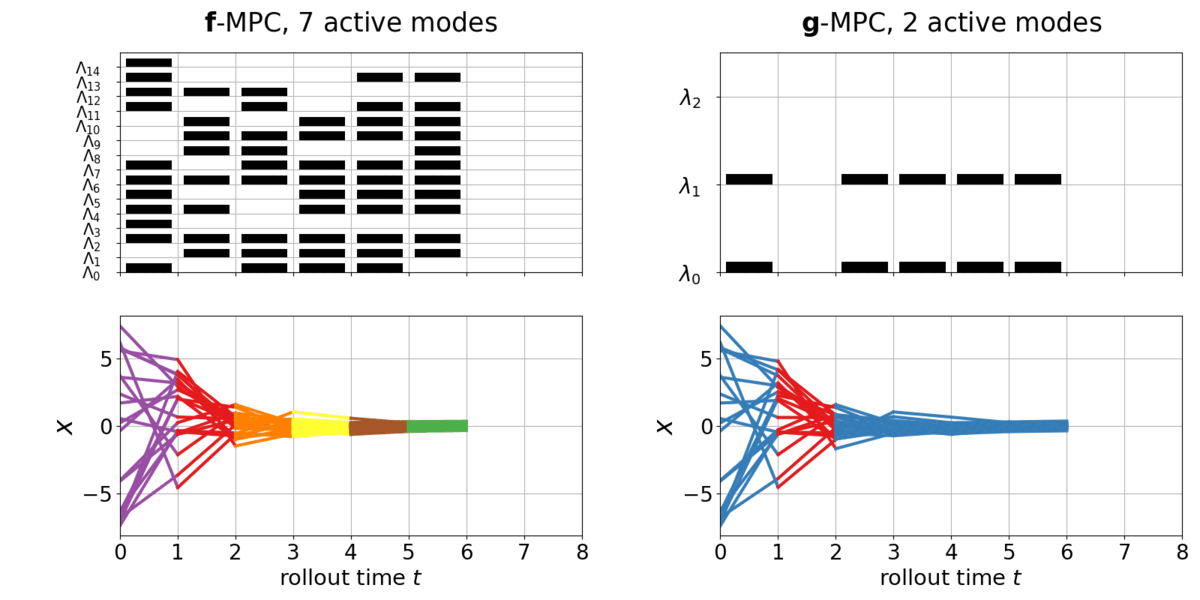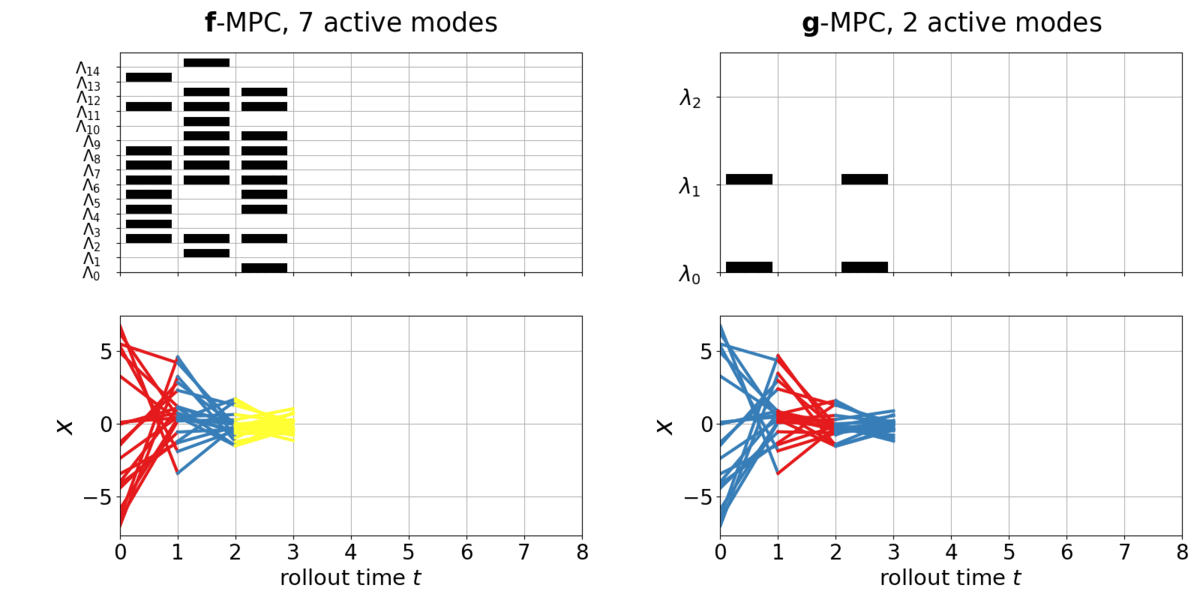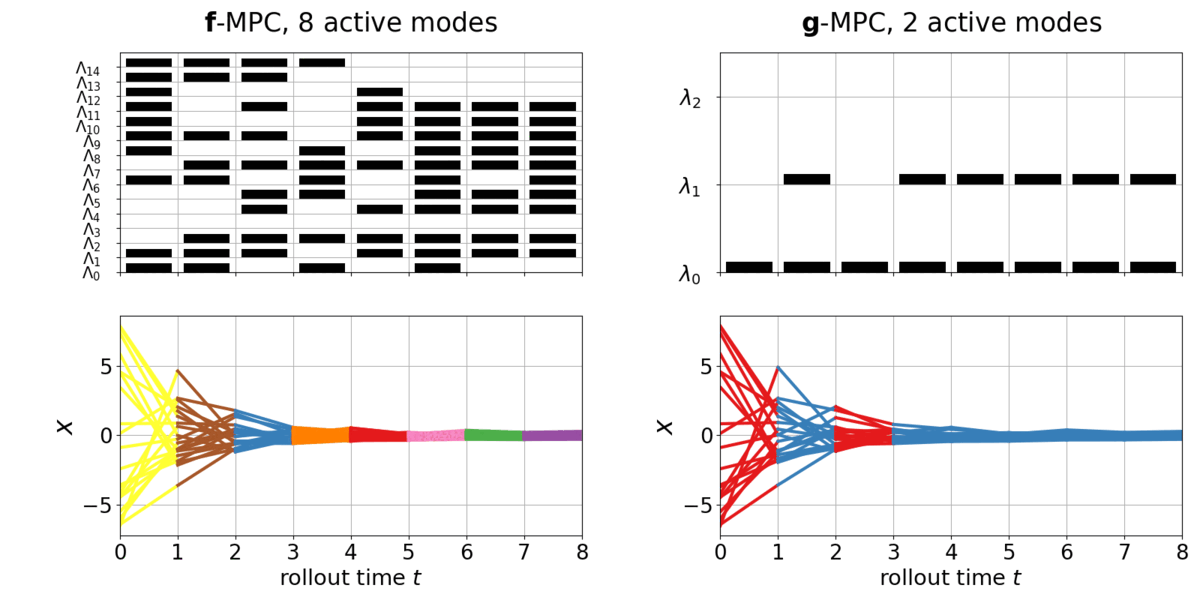
Upper: the mode activation in each dimension of \(\boldsymbol{\Lambda}\) in \(\boldsymbol{f}()\) and in each dimension \(\boldsymbol{\lambda}\) in \(\color{red}\boldsymbol{g}()\) . Black indicate \(>0\) and blank indicate \(=0\). Lower: closed-loop state trajectory of \(\boldsymbol{f}\). Different colors indicate different modes.
Three-Finger Robotic Hand Manipulation
Manipulation Task 1: Cube Turning
The task is to let three robotic fingers turn the cube to any random orientation, sampled from \(\alpha^{\text{goal}}\sim U[−1.5, 1.5]\) (rad). No prior knowledge of the system dynamics model and no prior knowledge of the object is available. The system is estimated to have thousands of potential modes.
Learning without prior knowledge in 5 mins
With no prior knowledge about the system, our method learns a task-driven reduced-order LCS (with \(\color{red}\dim \boldsymbol{\lambda}=5\)) to solve the cube turning task with less than 5 mins of real data. The video here is the real-time running of the learned reduced-order MPC controller on the system.
Empirical correspondence between mode activation of LCS and physical contact interaction
An example rollout of running the learned reduced-order MPC controller on the three-finger manipulation system (0.1 x speed). Left: Mode activation in the learned reduced-order LCS (upper) and cube angle trajectory (lower) Right: physical contact interaction in the three-finger robotic hand manipulation
Robustness of the learned reduced-order MPC controller
We apply random (uniform distribution) external disturbance torque to the cube at each time step during the MPC policy rollout. Below, we vary the disturbance magnitude. Left: disturbance magnitude is 100 times the cube inertia, middle: disturbance magnitude is 1000 times the cube inertia, and right: disturbance magnitude is 5000 times the cube inertia.
Manipulation Task 2: Cube Moving
The task is to let three fingers move the cube to a random target pose \((\boldsymbol{p}^{\text{goal}}, \alpha^{\text{goal}})\), where the target position and angle are sampled from \(\boldsymbol{p}^{\text{goal}}\sim U[−0.06, 0.06]\) (m) and \(\alpha^{\text{goal}}\sim U[−1.5, 1.5]\) (rad), respectively. No prior knowledge of the system dynamics model and no prior knowledge of the object is available. The system is estimated to have thousands of potential modes.
Learning with no prior knowledge within 5 minutes
With no prior knowledge, our method learns a reduced-order LCS (with \(\color{red}\dim \boldsymbol{\lambda}=5\)) to solve the task with less than 5 mins of real data. The video here is the real-time running of the learned reduced-order MPC controller on the system.
Different contact strategies for different targets
The following videos show different contact strategies generated by the same learned reduced-order LCS in its MPC rollout given different targets. Notably, as shown here, for different targets, the learned reduced-order LCS can produce different contact strategies between fingertips and the cube, such as separate, slip, and stick, and different decisions about which fingertip touches which face of the cube.
Robustness of the learned reduced-order MPC controller
We apply random (uniform distribution) external disturbance forces to the cube at each time step during the reduced-order MPC rollout. Below, we vary the disturbance magnitude. Left: the disturbance magnitude is 0.4 times the cube mass, middle: the disturbance magnitude is 0.7 times the cube mass, and right: the disturbance magnitude is 1.0 times the cube mass,
Final remarks: for more technical details and experiments, please check out our paper and code.
Acknowledgements
Toyota Research Institute provided funds to support this work.
