Wanxin Jin (靳万鑫)

I am an Assistant Professor in the School for Engineering of Matter, Transport and Energy at Arizona State University (ASU). I lead the Intelligent Robotics and Interactive Systems (IRIS) Lab. I teach robotics at ASU.

Prior to ASU, I was a Postdoctoral Researcher in the GRASP Lab, University of Pennsylvania, working with Dr. Michael Posa. I obtained my Ph.D. from Purdue University in 2021, working with Dr. Shaoshuai Mou. I was a research assistant at Technical University of Munich in 2016 and 2017, working with Dr. Sandra Hirche.

                   

---

My Research

The research of our Intelligent Robotics and Interactive Systems (IRIS) Lab is focused on

• Human-autonomy alignment: We develop certifiable, efficient, and empowering methods to enable robots to align their autonomy with human users through various natural interactions.

• Contact-rich dexterous manipulation: We develop efficient physics-based representations/modeling, planning/control methods to enable robots to gain dexterity through frequently making or breaking contacts with objects.

• Fundamental computational methods: We develop fundamental algorithms for efficient, safe, and robust robot intelligence, by harnessing the complementary benefits of model-based and data-driven approaches.

---

Highlighted Research and Publications

1. Contact-rich dexterous manipulation

---

ContactSDF: Signed Distance Functions as Multi-Contact Models for Dexterous Manipulation
Wen Yang and Wanxin Jin
Submitted to IEEE Robotics and Automation Letters (RA-L), 2024, 2024
[PDF]/ [Code]/ [Video]/ [Webpage]

---

Complementarity-Free Multi-Contact Modeling and Optimization for Dexterous Manipulation
Wanxin Jin
arXiv preprint, 2024
[PDF]/ [Code]/ [Video]

---

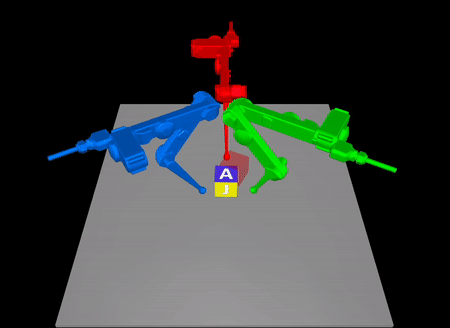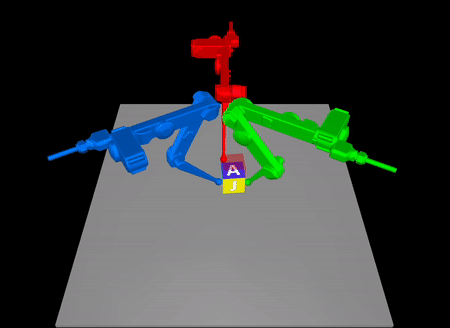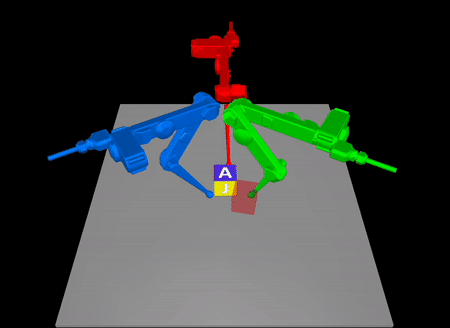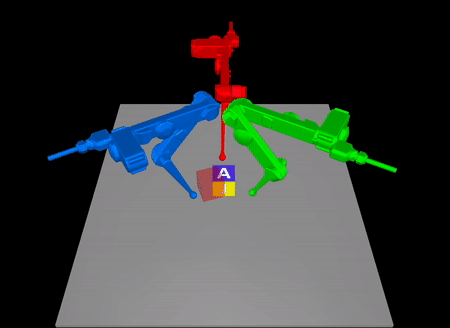
Task-Driven Hybrid Model Reduction for Dexterous Manipulation
Wanxin Jin and Michael Posa
IEEE Transactions on Robotics (T-RO), 2024
[PDF]/ [Code]/ [Video]/ [Webpage]

---

Adaptive Contact-Implicit Model Predictive Control with Online Residual Learning
Wei-Cheng Huang, Alp Aydinoglu, Wanxin Jin, Michael Posa
IEEE International Conference on Robotics and Automation (ICRA), 2024
[PDF]/ [Code]/ [Video]/ [Webpage]

---

Learning Linear Complementarity Systems
Wanxin Jin, Alp Aydinoglu, Mathew Halm, and Michael Posa
Learning for Dynamics and Control (L4DC), 2022
[PDF] / [Code]

---

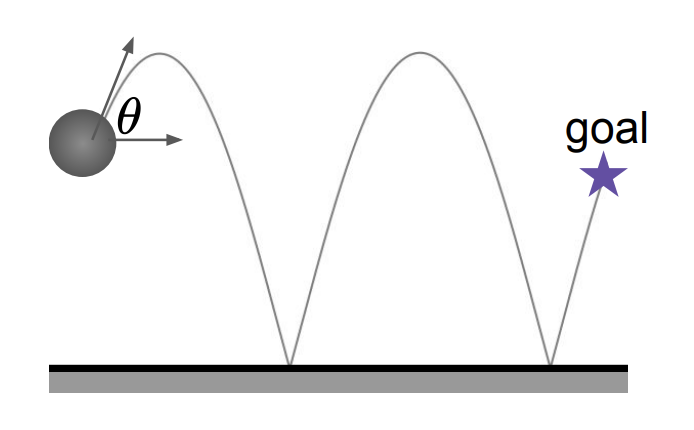Adaptive Barrier Smoothing for First-Order Policy Gradient with Contact Dynamics
Shenao Zhang, Wanxin Jin, Zhaoran Wang
International Conference on Machine Learning (ICML), 2023
[PDF]

2. Human-autonomy alignment

---

Language-Model-Assisted Bi-Level Programming for Reward Learning from Internet Videos
Harsh Mahesheka, Zhixian Xie, Zhaoran Wang, and Wanxin Jin
arXiv preprint, 2024
[PDF] / [Videos]/

---

Safe MPC Alignment with Human Directional Feedback
Zhixian Xie, Wenlong Zhang, Yi Ren, Zhaoran Wang, George. J. Pappas, and Wanxin Jin
Submitted to IEEE Transactions on Robotics (T-RO), 2024
[PDF] / [Code] / [Videos]/ [Webpage]

---

Learning from Human Directional Corrections
Wanxin Jin, Todd D Murphey, and Shaoshuai Mou
IEEE Transactions on Robotics (T-RO), 2022
[PDF] / [Code] / [Videos]

---

Learning from Sparse Demonstrations
Wanxin Jin, Todd D Murphey, Dana Kulic, Neta Ezer, and Shaoshuai Mou
IEEE Transactions on Robotics (T-RO), 2022
[PDF]/ [Code] / [Videos]

---

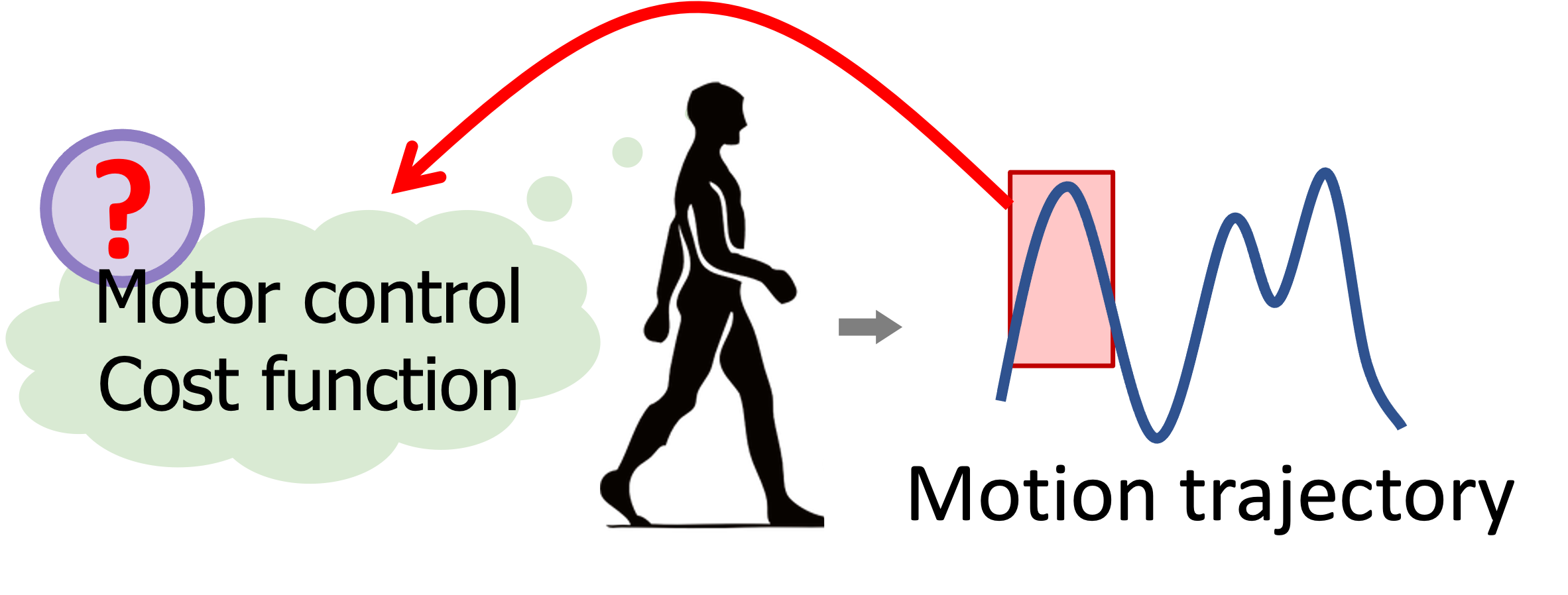Inverse Optimal Control from Incomplete Trajectory Observations
Wanxin Jin, Dana Kulic, Shaoshuai Mou, and Sandra Hirche
International Journal of Robotics Research (IJRR), 40:848–865, 2021
[PDF] / [Code]

---

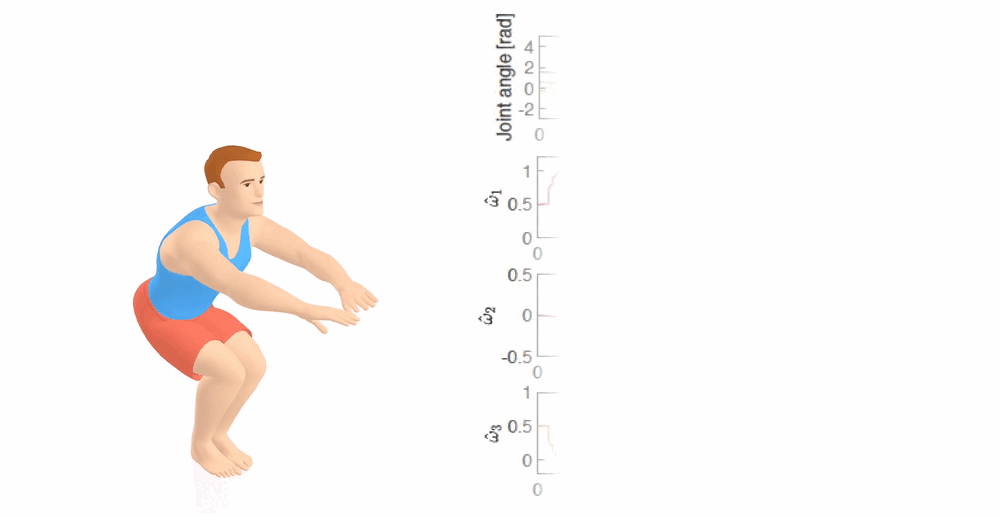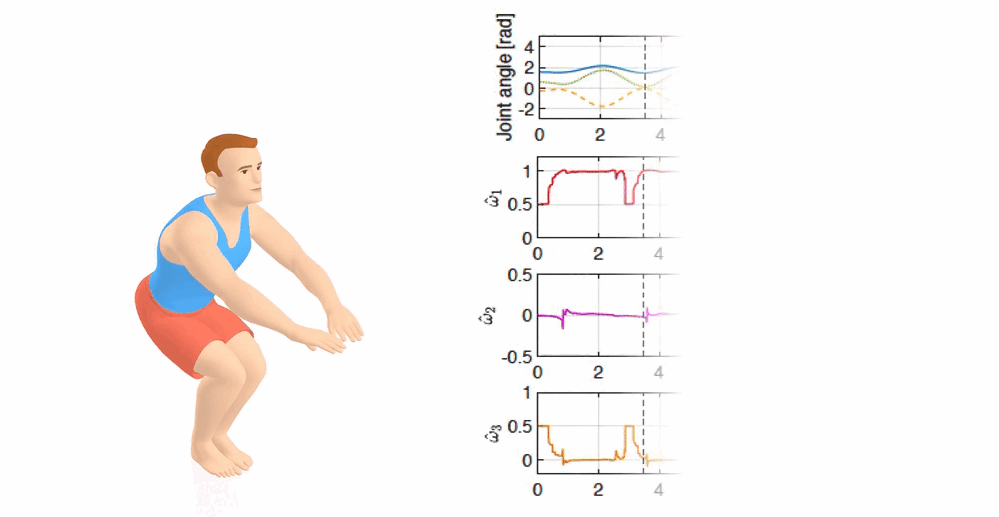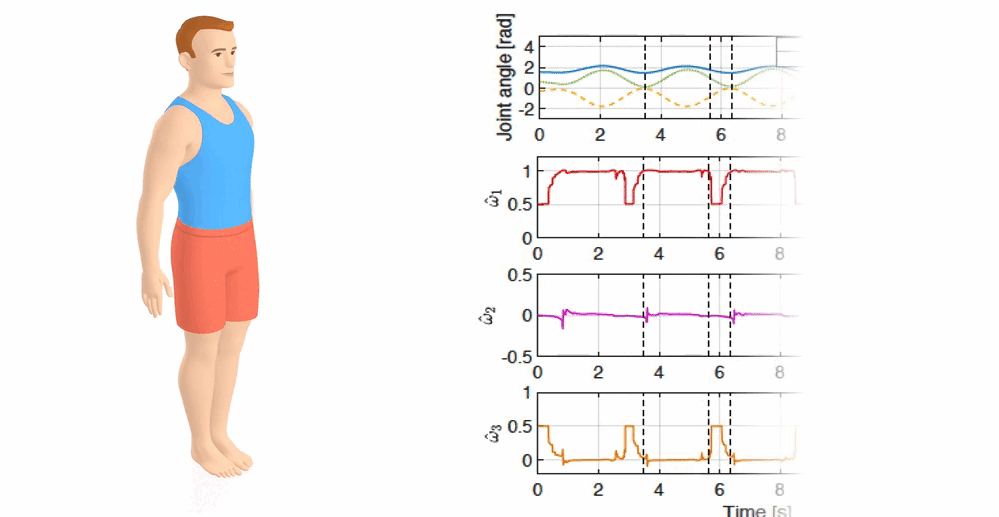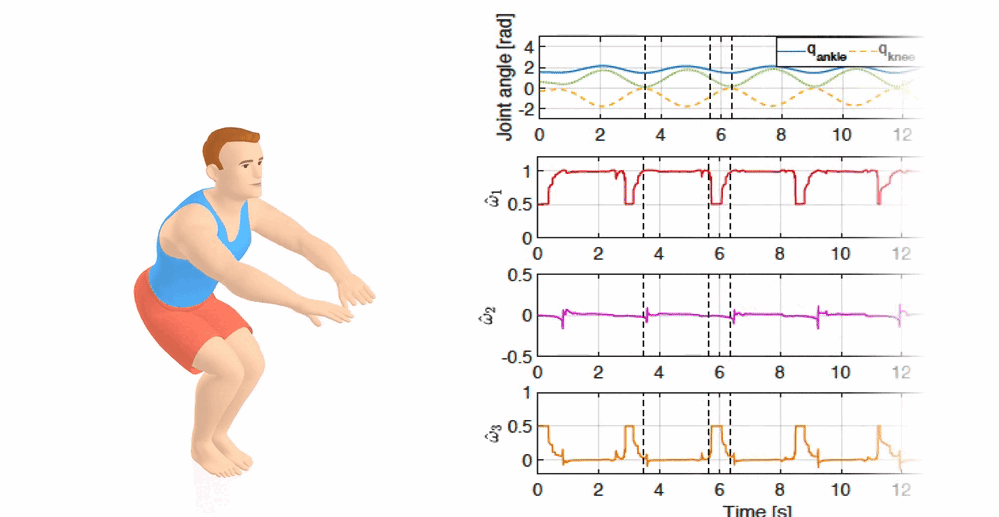Inverse Optimal Control for Multiphase cost functions
Wanxin Jin, Dana Kulic, Jonathan Lin, Shaoshuai Mou, and Sandra Hirche
IEEE Transactions on Robotics (T-RO), 35(6):1387–1398, 2019
[PDF] / [Code]

3. Fundamental computational methods

---

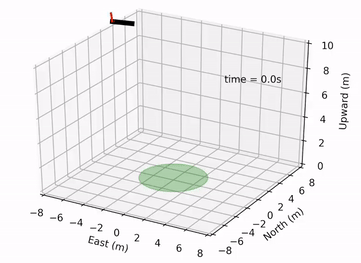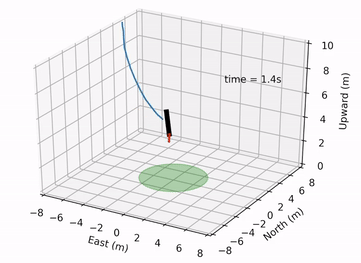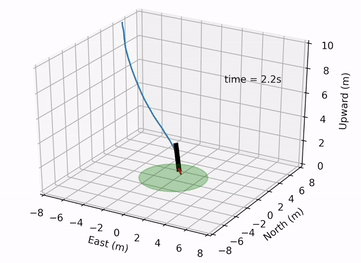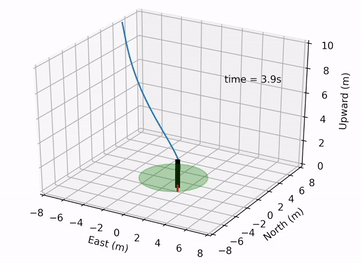Pontryagin Differentiable Programming: An End-to-End Learning and Control Framework
Wanxin Jin, Zhaoran Wang, Zhuoran Yang, and Shaoshuai Mou
Advances in Neural Information Processing Systems (NeurIPS), 2020
[PDF] / [Code] / [Videos]/ [Webpage]

---

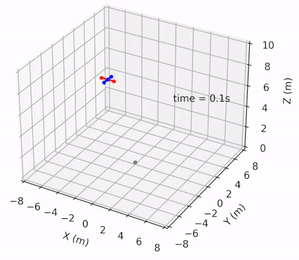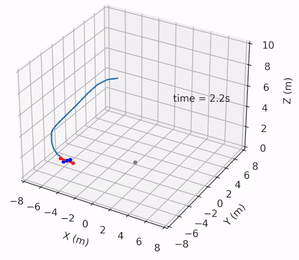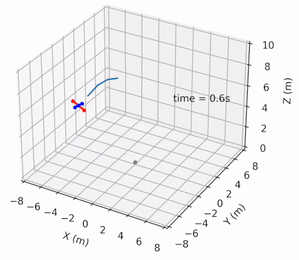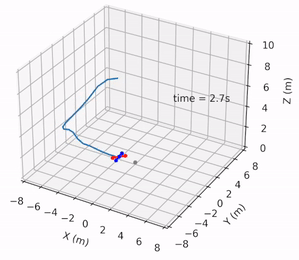Safe Pontryagin Differentiable Programming
Wanxin Jin, Shaoshuai Mou, and George J. Pappas
Advances in Neural Information Processing Systems (NeurIPS), 2021
[PDF] / [Code] / [Videos]/ [Webpage]

---

A Differential Dynamic Programming Framework for Inverse Reinforcement Learning
Kun Cao, Xinhang Xu, Wanxin Jin, Karl H. Johansson, and Lihua Xie
Submitted to IEEE Transactions on Robotics (T-RO), 2024
[PDF]

---

Robust Safe Learning and Control in Unknown Environments: An Uncertainty-Aware Control Barrier Function Approach
Jiacheng Li, Qingchen Liu, Wanxin Jin, Jiahu Qin, and Sandra Hirche
IEEE Robotics and Automation Letters (RA-L), 2023
[PDF] / [Videos]

---

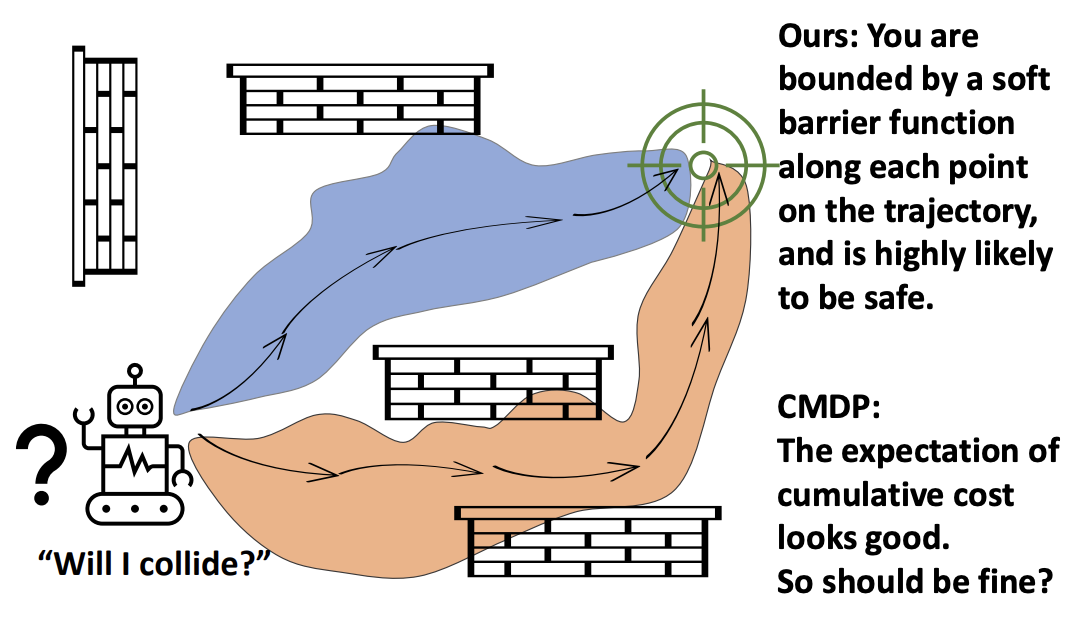Enforcing Hard Constraints with Soft Barriers: Safe-driven Reinforcement Learning in Unknown Stochastic Environments
Yixuan Wang, Simon Sinong Zhan, Ruochen Jiao, Zhilu Wang, Wanxin Jin, Zhuoran Yang, Zhaoran Wang, Chao Huang, Qi Zhu
International Conference on Machine Learning (ICML), 2023
[PDF]