Derivative of Transformation

Consider a time-varying rotation matrix \(\boldsymbol{R}=\boldsymbol{R}(t)\). One has

\[\boldsymbol{R}(t) \boldsymbol{R}^{T}(t)=\boldsymbol{I}\]

Differentiating the above equation with respect to time gives

\[\dot{\boldsymbol{R}}(t) \boldsymbol{R}^{T}(t)+\boldsymbol{R}(t) \dot{\boldsymbol{R}}^{T}(t)=\boldsymbol{S}(t)+\boldsymbol{S}^{T}(t)=\boldsymbol{O}\]

with the newly defined \(\boldsymbol{S}(t)=\dot{\boldsymbol{R}}(t) \boldsymbol{R}^{T}(t)\) being called a \((3 \times 3)\) skew-symmetric matrix, and

\[\dot{\boldsymbol{R}}(t)=\boldsymbol{S}(t) \boldsymbol{R}(t)\]

Next, let’s find the physical interpretation of \(\boldsymbol{S}\).

Consider \({\boldsymbol{R}}(t)\) represents a rotation of a moving frame \(O'-x'y'z'\) with respect to a fixed reference frame \(O-xyz\). It means the following coordinate transformation \(\boldsymbol{p}(t)=\boldsymbol{R}(t) \boldsymbol{p}^{\prime}\). Taking the derivative of both sides yields

\[\dot{\boldsymbol{p}}(t)=\dot{\boldsymbol{R}}(t) \boldsymbol{p}^{\prime}=\boldsymbol{S}(t) \boldsymbol{R}(t) \boldsymbol{p}^{\prime}\]

where we have used the defined skew-symmetric matrix \(\boldsymbol{S}(t)\), and considered \(\boldsymbol{p}^\prime\) is fixed in the moving frame.

Recall that in the mechanics courses, given the angular velocity \(\boldsymbol{\omega}(t)=\left[\begin{array}{lll}\omega_{x} & \omega_{y} & \omega_{z}\end{array}\right]^{T}\) of the moving frame \(O'-x'y'z'\), with respect to the fixed frame, we also write the derivative as

\[\dot{\boldsymbol{p}}(t)=\boldsymbol{\omega}(t) \times \boldsymbol{R}(t) \boldsymbol{p}^{\prime}\]

Comparing the above two equations, we can conclude

\[\begin{split}\boldsymbol{S}=\left[\begin{array}{ccc} 0 & -\omega_{z} & \omega_{y} \\ \omega_{z} & 0 & -\omega_{x} \\ -\omega_{y} & \omega_{x} & 0 \end{array}\right]=\boldsymbol{S}(\boldsymbol{\omega})\end{split}\]

Hence, we can conclude the derivative of a rotation matrix is $\(\dot{\boldsymbol{R}}=\boldsymbol{S}(\boldsymbol{\omega}) \boldsymbol{R}\)$

Note that in the above equation, \(\boldsymbol{\omega}\) is expressed in the fixed frame.

One property of \(\boldsymbol{S}(\boldsymbol{\omega})\): if \(\boldsymbol{R}\) denotes a rotation matrix, it can be shown that the following relation holds:

\[\boldsymbol{R} \boldsymbol{S}(\boldsymbol{\omega}) \boldsymbol{R}^{T}=\boldsymbol{S}(\boldsymbol{R} \boldsymbol{\omega})\]

Derivative of Pose Transformation

Pose transformation defines coordinate mapping of a point \(P\) from frame \(O_1-x_1y_1z_1\) to frame \(O_0-x_0y_0z_0\)

\[\boldsymbol{p}^{0}=\boldsymbol{o}_{1}^{0}+\boldsymbol{R}_{1}^{0} \boldsymbol{p}^{1}\]

Differentiating the above equation with respect to time yields

\[\dot{\boldsymbol{p}}^{0}=\dot{\boldsymbol{o}}_{1}^{0}+\boldsymbol{R}_{1}^{0} \dot{\boldsymbol{p}}^{1}+\dot{\boldsymbol{R}}_{1}^{0} \boldsymbol{p}^{1}=\dot{\boldsymbol{o}}_{1}^{0}+\boldsymbol{R}_{1}^{0} \dot{\boldsymbol{p}}^{1}+\boldsymbol{S}\left(\boldsymbol{\omega}_{1}^{0}\right) \boldsymbol{R}_{1}^{0} \boldsymbol{p}^{1}\]

Since \(\boldsymbol{R}_{1}^{0} \boldsymbol{p}^{1}=\boldsymbol{p}_{1}^{0}\),

\[\dot{\boldsymbol{p}}^{0}=\dot{\boldsymbol{o}}_{1}^{0}+\boldsymbol{R}_{1}^{0} \dot{\boldsymbol{p}}^{1}+\omega_{1}^{0} \times \boldsymbol{r}_{1}^{0}\]

Notice that, if \(\boldsymbol{p}^{1}\) is fixed in Frame 1 , then it is

\[\dot{\boldsymbol{p}}^{0}=\dot{\boldsymbol{o}}_{1}^{0}+\boldsymbol{\omega}_{1}^{0} \times \boldsymbol{r}_{1}^{0}\]

Manipulator Link Velocity

Consider the Link \(i\) of a manipulator. According to DH convention, the pose of Link \(i\) defines the transformation between Frame \(i-1\) and Frame \(i\), as shown in the following figure below.

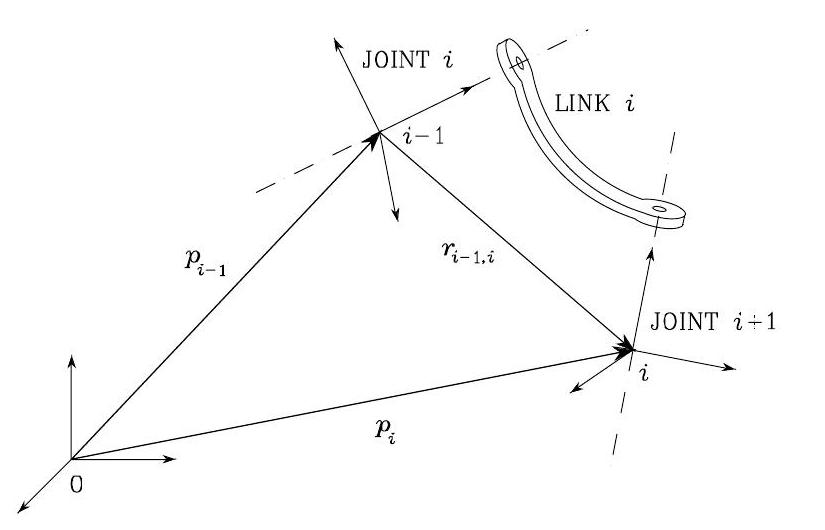
Fig. 48 Characterization of generic Link \(i\) of a manipulator

Linear Velocity

Let \(\boldsymbol{p}_{i-1}\) and \(\boldsymbol{p}_{i}\) be the position of the origins of Frames \(i-1\) and \(i\), respectively. Also, let \(\boldsymbol{r}_{i-1, i}^{i-1}\) denote the position of the origin of Frame \(i\) with respect to Frame \(i-1\) expressed in Frame \(i-1\).

\[\boldsymbol{p}_{i}=\boldsymbol{p}_{i-1}+\boldsymbol{R}_{i-1} \boldsymbol{r}_{i-1, i}^{i-1}\]

Based on the derivative of pose transformation, we have

\[\dot{\boldsymbol{p}}_{i}=\dot{\boldsymbol{p}}_{i-1}+\boldsymbol{R}_{i-1} \dot{\boldsymbol{r}}_{i-1, i}^{i-1}+\boldsymbol{\omega}_{i-1} \times \boldsymbol{R}_{i-1} \boldsymbol{r}_{i-1, i}^{i-1}=\dot{\boldsymbol{p}}_{i-1}+\boldsymbol{v}_{i-1, i}+\omega_{i-1} \times \boldsymbol{r}_{i-1, i}\]

which gives the linear velocity of Link \(i\) as a function of the translational and rotational velocities of Link \(i-1\).

Angular Velocity

Since

\[\boldsymbol{R}_{i}=\boldsymbol{R}_{i-1} \boldsymbol{R}_{i}^{i-1}\]

Its time derivative

\[\boldsymbol{S}\left(\boldsymbol{\omega}_{i}\right) \boldsymbol{R}_{i}=\boldsymbol{S}\left(\boldsymbol{\omega}_{i-1}\right) \boldsymbol{R}_{i}+\boldsymbol{R}_{i-1} \boldsymbol{S}\left(\boldsymbol{\omega}_{i-1, i}^{i-1}\right) \boldsymbol{R}_{i}^{i-1}\]

where \(\boldsymbol{\omega}_{i-1, i}^{i-1}\) denotes the angular velocity of Frame \(i\) with respect to Frame \(i-1\) expressed in Frame \(i-1\). The second term on the right-hand side can be rewritten as

\[\boldsymbol{R}_{i-1} \boldsymbol{S}\left(\boldsymbol{\omega}_{i-1, i}^{i-1}\right) \boldsymbol{R}_{i}^{i-1}=\boldsymbol{R}_{i-1} \boldsymbol{S}\left(\boldsymbol{\omega}_{i-1, i}^{i-1}\right) \boldsymbol{R}_{i-1}^{T} \boldsymbol{R}_{i-1} \boldsymbol{R}_{i}^{i-1}=\boldsymbol{S}\left(\boldsymbol{R}_{i-1} \boldsymbol{\omega}_{i-1, i}^{i-1}\right) \boldsymbol{R}_{i}\]

by recalling the property of the skew-symmetric matrix. Then,

\[\boldsymbol{S}\left(\boldsymbol{\omega}_{i}\right) \boldsymbol{R}_{i}=\boldsymbol{S}\left(\boldsymbol{\omega}_{i-1}\right) \boldsymbol{R}_{i}+\boldsymbol{S}\left(\boldsymbol{R}_{i-1} \boldsymbol{\omega}_{i-1, i}^{i-1}\right) \boldsymbol{R}_{i}\]

leading to

\[\boldsymbol{\omega}_{i}=\boldsymbol{\omega}_{i-1}+\boldsymbol{R}_{i-1} \boldsymbol{\omega}_{i-1, i}^{i-1}=\boldsymbol{\omega}_{i-1}+\boldsymbol{\omega}_{i-1, i}\]

which gives the expression of the angular velocity of Link \(i\) as a function of the angular velocities of Link \(i-1\) and of Link \(i\) with respect to Link \(i-1\).

Summary

Considering different types of Joint \(i\), according to the above derivative of linear velocity and angular velocity, we have the following conclusions.

If Joint \(i\) is prismatic

\[\begin{split}\begin{aligned} \boldsymbol{\omega}_{i} & =\boldsymbol{\omega}_{i-1} \\ \dot{\boldsymbol{p}}_{i} & =\dot{\boldsymbol{p}}_{i-1}+\dot{d}_{i} \boldsymbol{z}_{i-1}+\boldsymbol{\omega}_{i} \times \boldsymbol{r}_{i-1, i} \end{aligned}\end{split}\]

If Joint \(i\) is revolute

\[\begin{split}\begin{aligned} \boldsymbol{\omega}_{i} & =\boldsymbol{\omega}_{i-1}+\dot{\vartheta}_{i} \boldsymbol{z}_{i-1} \\ \dot{\boldsymbol{p}}_{i} & =\dot{\boldsymbol{p}}_{i-1}+\boldsymbol{\omega}_{i} \times \boldsymbol{r}_{i-1, i} \end{aligned}\end{split}\]