Robot Configuration

Fig. 5 Franka Emika Panda robot arm

A robot manipulator is mechanically constructed by

• a set of rigid bodies, each body called a link,

• joints, connecting two consecutive links and providing motion constraints (degrees of freedom)

  

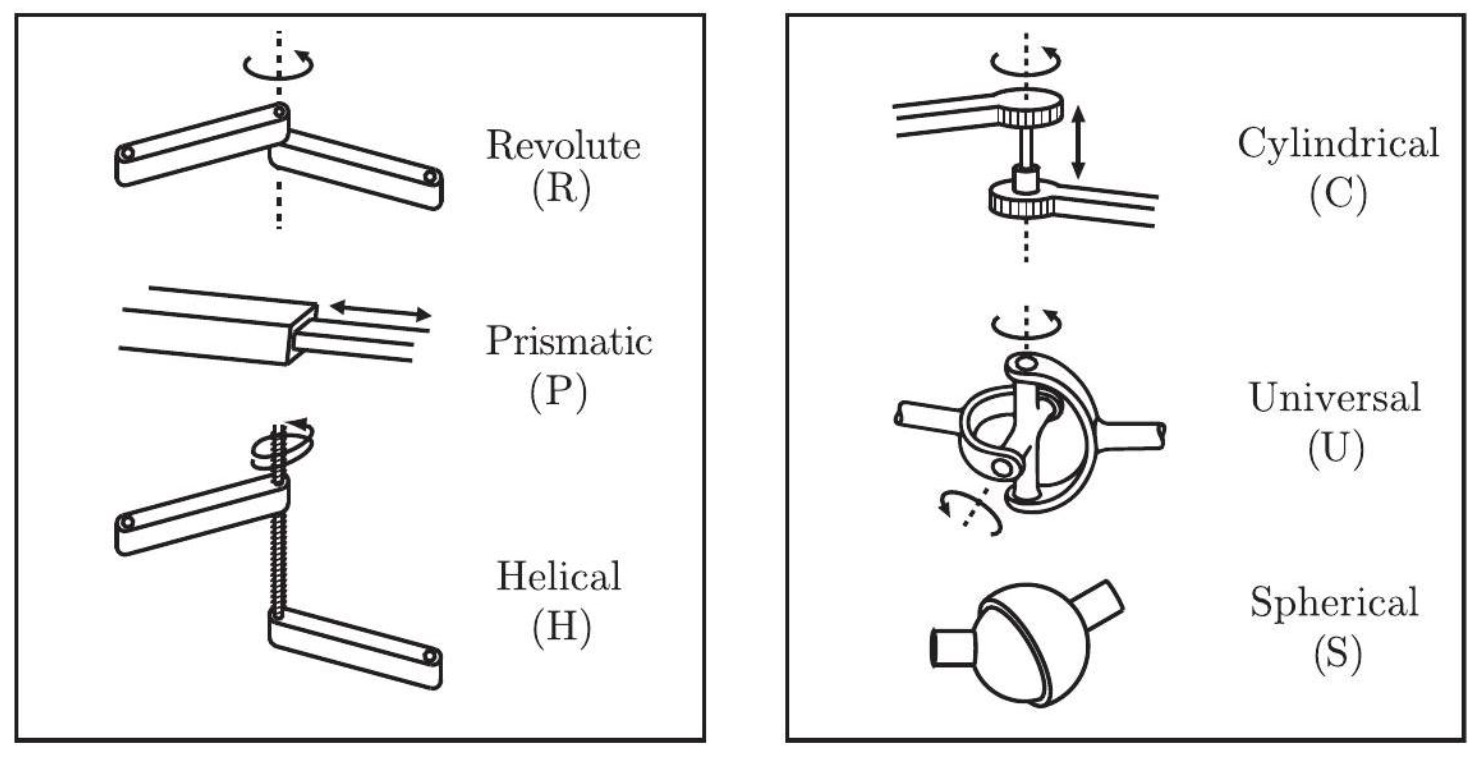
  Fig. 6 Different type of joints

• actuators, such as electric/hydraulic/pneumatic actuators, deliver forces or torques that cause the robot’s links to move,

  

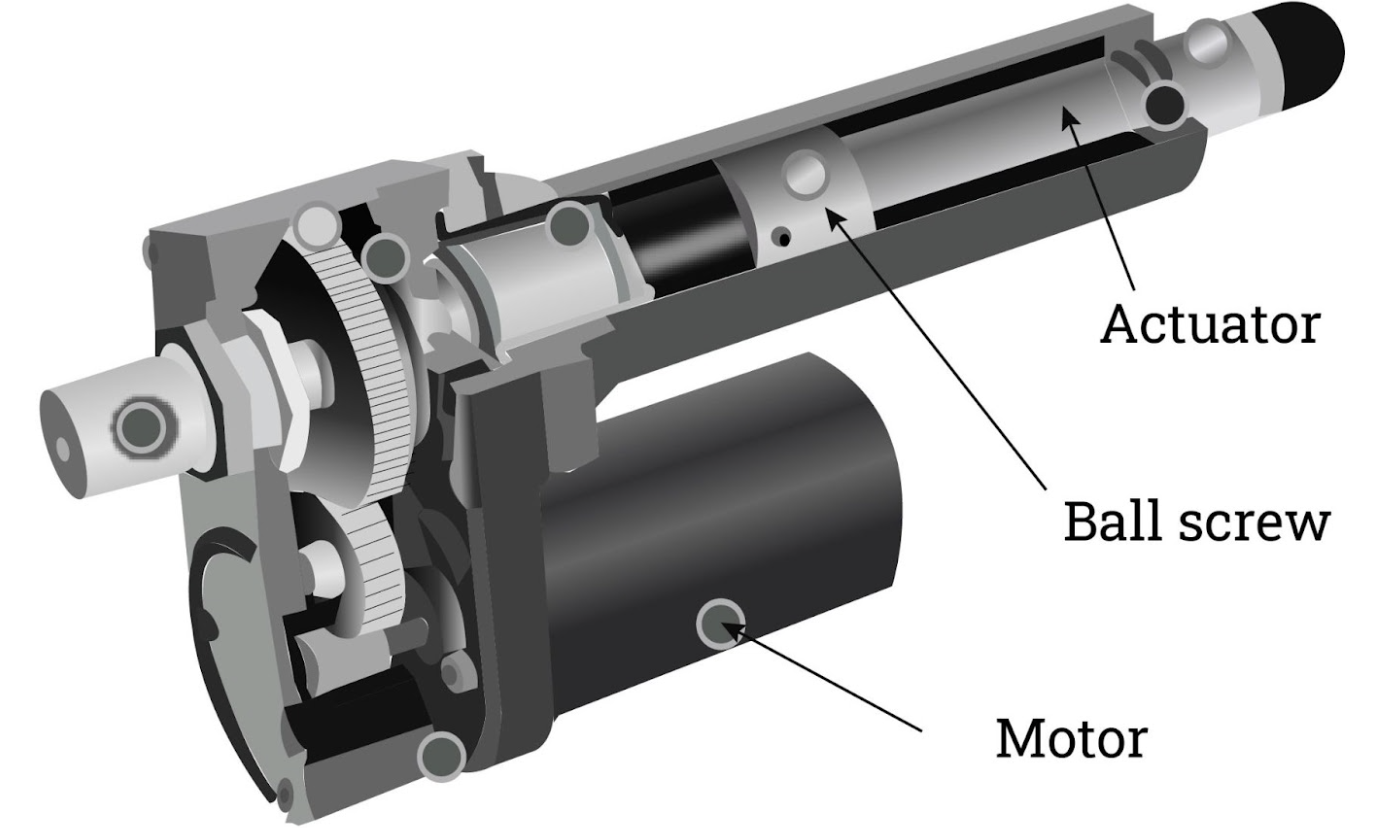
  Fig. 7 Electric actuators

  

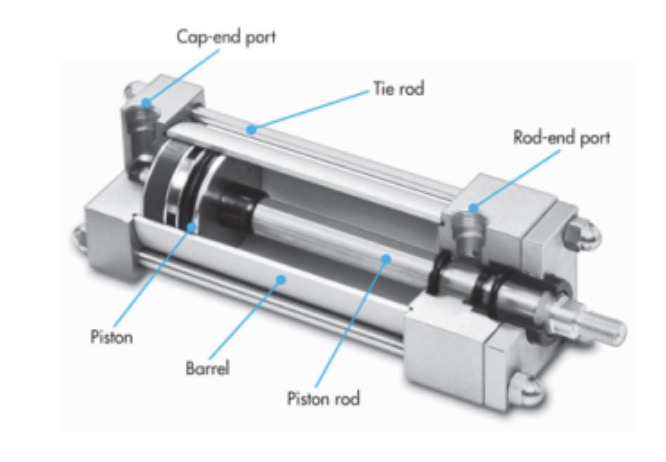
  Fig. 8 Hydralic actuator

• an end effector, such as a gripper or hand, is attached to a specific link for specific tasks.

  

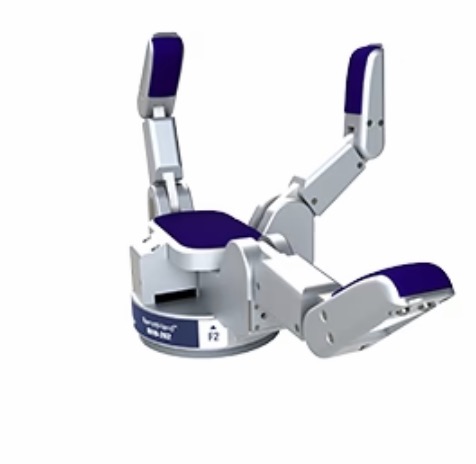
  Fig. 9 The Barrett Hand

  

  Fig. 10 The Shadow Hand

The fundamental structure of a manipulator is the serial or open kinematic chain. From a topological viewpoint, a kinematic chain is termed open when there is only one sequence of links connecting the two ends of the chain. Alternatively, a manipulator contains a closed kinematic chain when a sequence of links forms a loop.

Configuration

Important

The configuration of a robot is a complete specification of the position of every point of the robot. Since the robot’s links are rigid and of a known shape, only a few variables (coordinates in a general sense) can be selected to represent its configuration.

For example, in the following figure, the configuration of a door can be represented by a single variable, the hinge angle \(\theta\). The configuration of a point on a plane can be described by two coordinates, \((x, y)\). The configuration of a coin lying heads up on a flat table can be described by three coordinates: two coordinates \((x, y)\) that specify the location of a particular point on the coin, and one coordinate \((\theta)\) that specifies the coin’s orientation.

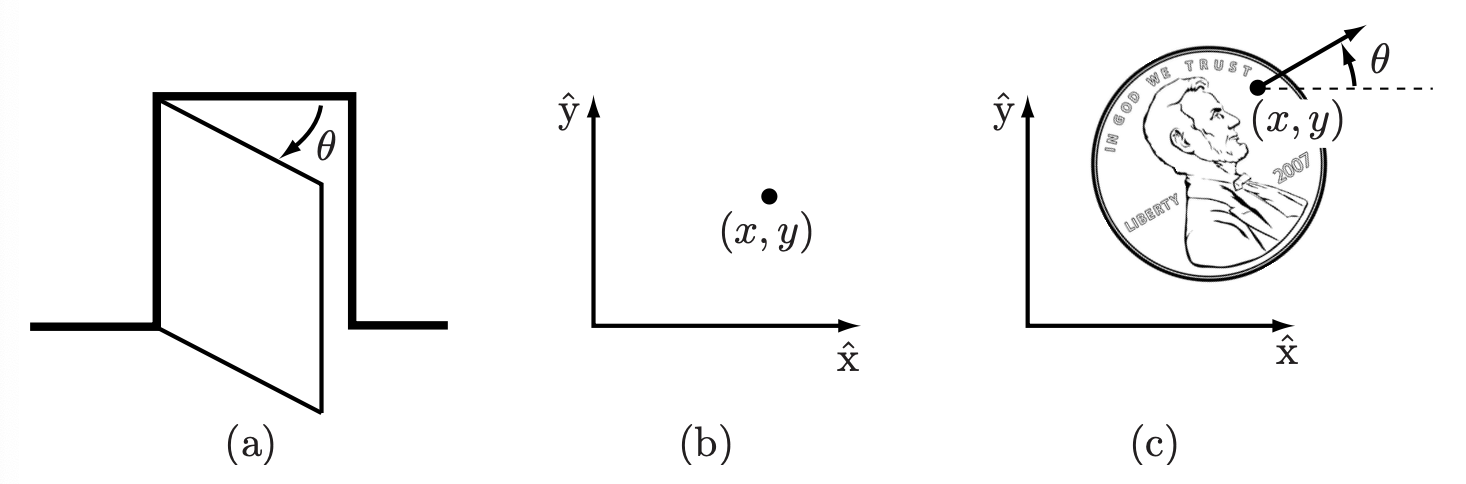
Fig. 11 (a) The configuration of a door is described by the angle \(\theta\). (b) The configuration of a point in a plane is described by coordinates \((x, y)\). (c) The configuration of a coin (heads up) on a table is described by \((x, y, \theta)\), where \(\theta\) defines the direction in which Abraham Lincoln is looking.

Important

The minimum number \(n\) of real-valued coordinates needed to represent the configuration is the number of degrees of freedom (dof) of the robot. The \(n\)-dimensional space containing all possible configurations of the robot is called the configuration space (C-space). The configuration of a robot is represented by a point in its C-space.

Degrees of Freedom

General Rule

We have the following general rule for determining the number of degrees of freedom of a system:

Important

degrees of freedom = number of variables - number of independent equations (constraints)

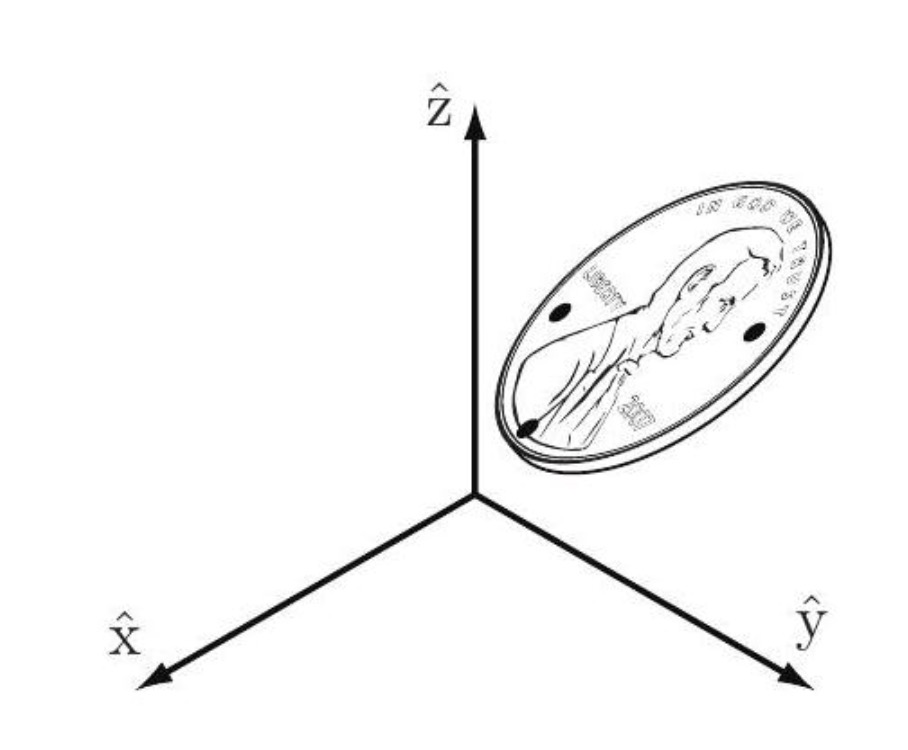
Fig. 12 Degrees of freedom of a coin in 3D space

Example: consider a coin in 3D space in Fig. 8{reference-type=”ref” reference=”c1.fig.3dcoin”}, the coordinates for the three points \(A, B\), and \(C\) are given by \(\left(x_{A}, y_{A}, z_{A}\right),\left(x_{B}, y_{B}, z_{B}\right)\), and \(\left(x_{C}, y_{C}, z_{C}\right)\), respectively. Point \(A\) can be placed freely (three degrees of freedom). The location of point \(B\) is subject to the constraint \(d(A, B)=d_{A B}\), meaning it must lie on the sphere of radius \(d_{A B}\) centered at \(A\). Thus we have \(3-1=2\) freedoms to specify, which can be expressed as the latitude and longitude for the point on the sphere. Finally, the location of point \(C\) must lie at the intersection of spheres centered at \(A\) and \(B\) of radius \(d_{A C}\) and \(d_{B C}\), respectively. In the general case the intersection of two spheres is a circle, and the location of point \(C\) can be described by an angle that parametrizes this circle. Point \(C\) therefore adds \(3-2=1\) freedom. Once the position of point \(C\) is chosen, the coin is fixed in space. In summary, a rigid body in three-dimensional space has six freedoms, which can be described by the three coordinates parametrizing point \(A\), the two angles parametrizing point \(B\), and one angle parametrizing point \(C\), provided \(A, B\), and \(C\) are noncollinear.

• A rigid body moving in 3-dimensional space, which we call a spatial rigid body, has 6 degrees of freedom.

• A rigid body moving in a 2-dimensional plane, which we call a planar rigid body, has 3 degrees of freedom.

DOF for Different Joints

In typical robots, a joint can be viewed as providing freedoms to allow one rigid body to move relative to another. It can also be viewed as providing constraints on the possible motions of the two rigid bodies it connects. The following table summarizes the freedoms and constraints provided by the various joint types.

Joint type	dof \(f\)	Constraint counts between two spatial bodies
Revolute (R)	1	5
Prismatic (P)	1	2
Helical (H)	1	5
Cylindrical (C)	2	4
Universal (U)	2	4
Spherical (S)	3	3

Grübler’s Formula

Since our robots consist of rigid bodies, the degree of freedom of a robot can be expressed as follows:

Important

degrees of freedom = number of variables - number of independent equations (constraints)

Note

Consider a mechanism consisting of \(N\) links, where the ground is also regarded as a link. Let \(J\) be the number of joints, \(m\) be the number of degrees of freedom of a rigid body \((m=3\) for planar mechanisms and \(m=6\) for spatial mechanisms), \(f_{i}\) be the number of freedoms provided by joint \(i\), and \(c_{i}\) be the number of constraints provided by joint \(i\), where \(f_{i}+c_{i}=m\) for all \(i\). Then the Grübler’s formula for degrees of freedom of the robot is

\[\begin{split}\begin{aligned} \operatorname{dof} & =\underbrace{m(N-1)}_{\text {rigid body freedoms }}-\underbrace{\sum_{i=1}^{J} c_{i}}_{\text {joint constraints }} \\ & =m(N-1)-\sum_{i=1}^{J}\left(m-f_{i}\right) \\ & =m(N-1-J)+\sum_{i=1}^{J} f_{i} . \end{aligned}\end{split}\]

This formula holds only if all joint constraints are independent. If they are not independent then the formula provides a lower bound on the number of degrees of freedom. Below are some examples of using Grubler’s Formula to find the DoFs of different machenisms.

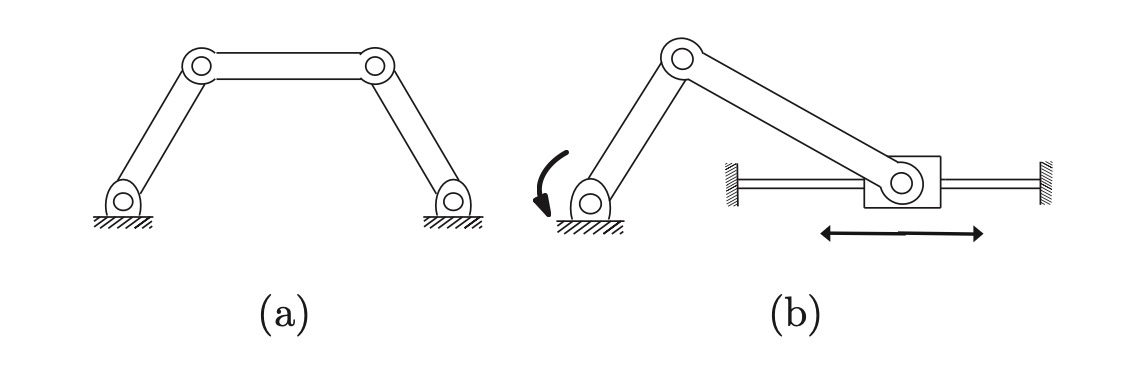
Fig. 13 (a) Four-bar linkage and (b) Slider-crank mechanism.

Four-bar linkage: \(N=4, J=4\), and \(f_{i}=1, i=1, \ldots, 4\). Thus, \(\operatorname{dof}\)=1.
Slider-crank: \(N=4\), \(J=4,\) and \(f_{i}=1, i=1, \ldots, 4\). Thus, \(\operatorname{dof}\)=1.

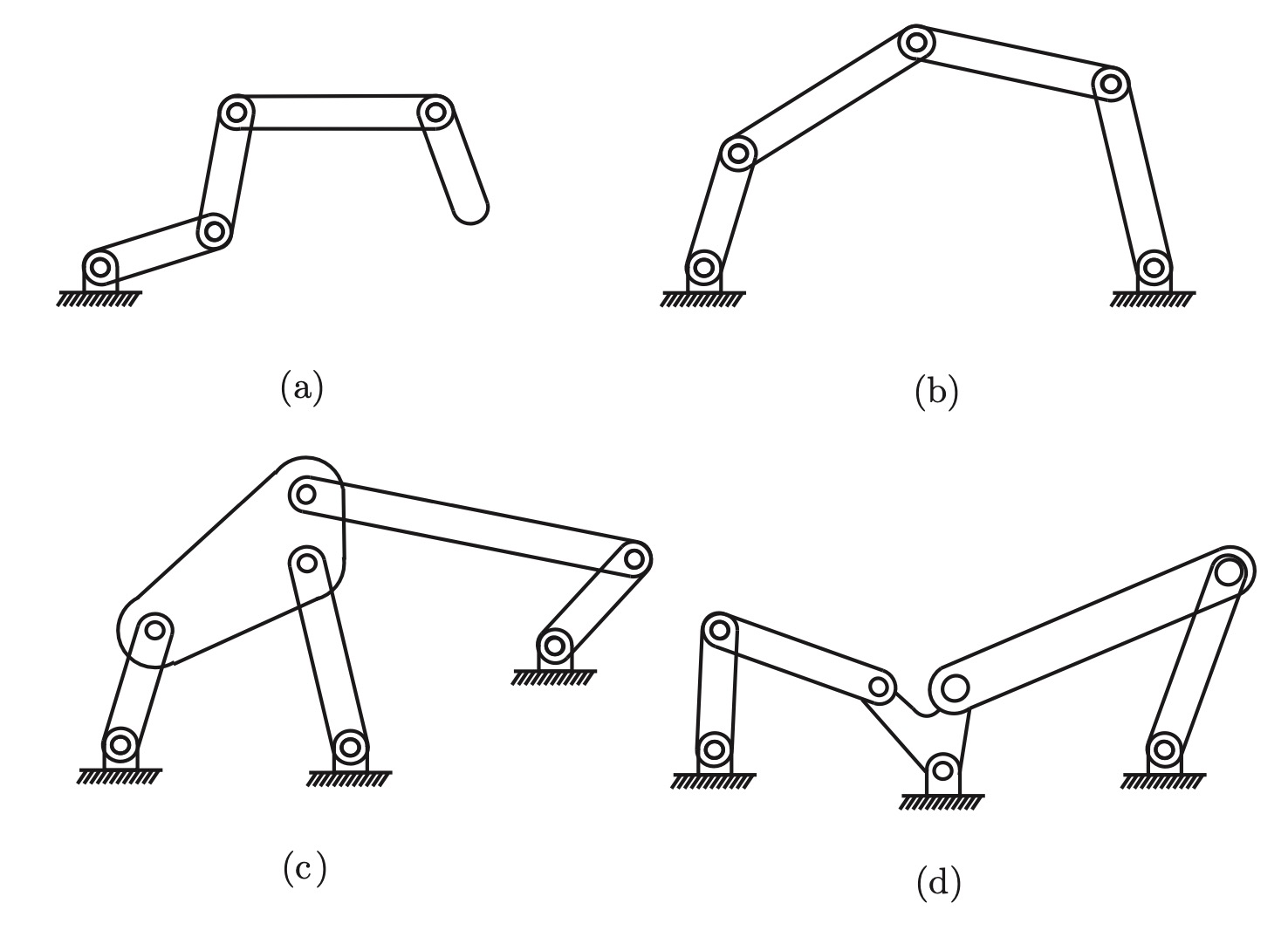
Fig. 14 (a) \(k\)-link planar serial chain. (b) Five-bar planar linkage. (c) Stephenson six-bar linkage. (d) Watt six-bar linkage.

The \(k\)-link planar robot: \(N=k+1\), \(J=k\), \(f_{i}=1\) for all \(i\). Thus, \(\operatorname{dof}=3((k+1)-1-k)+k=k\).
The five-bar linkage: \(N=5\), \(J=5\), each \(f_{i}=1\). Therefore, \(\operatorname{dof}=3(5-1-5)+5=2\).
Stephenson six-bar linkage: \(N=6, J=7\), and \(f_{i}=1\) for all \(i\). Therefore, \(\operatorname{dof}=3(6-1-7)+7=1\).
Watt six-bar linkage: \(N=6, J=7\), and \(f_{i}=1\) for all \(i\). Therefore, \(\operatorname{dof}=3(6-1-7)+7=1\).

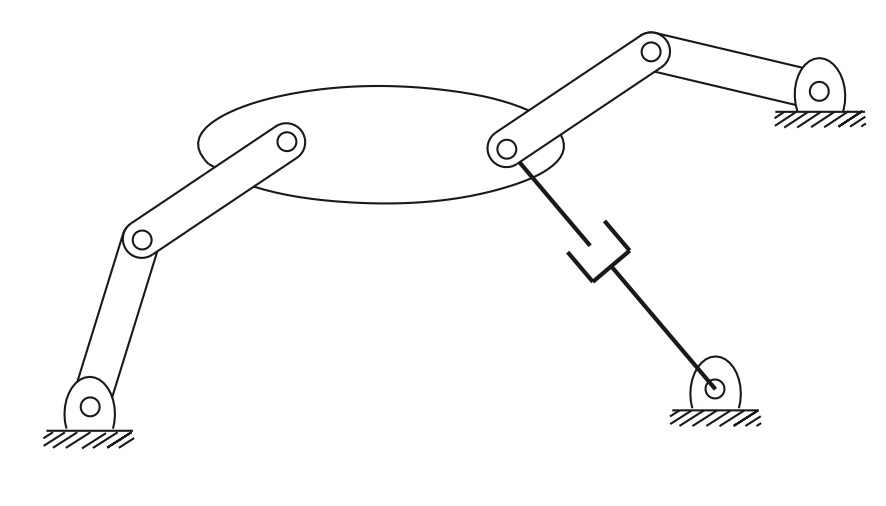
Fig. 15 A planar mechanism with two overlapping joints.

The planar mechanism illustrated has three links that meet at a single point on the right of the large link. Recalling that a joint by definition connects exactly two links, the joint at this point of intersection should not be regarded as a single revolute joint. Rather, it is correctly interpreted as two revolute joints overlapping each other. The mechanism consists of eight links \((N=8)\), eight revolute joints, and one prismatic joint. The Grübler’s formula:

\[\operatorname{dof}=3(8-1-9)+9(1)=3\]

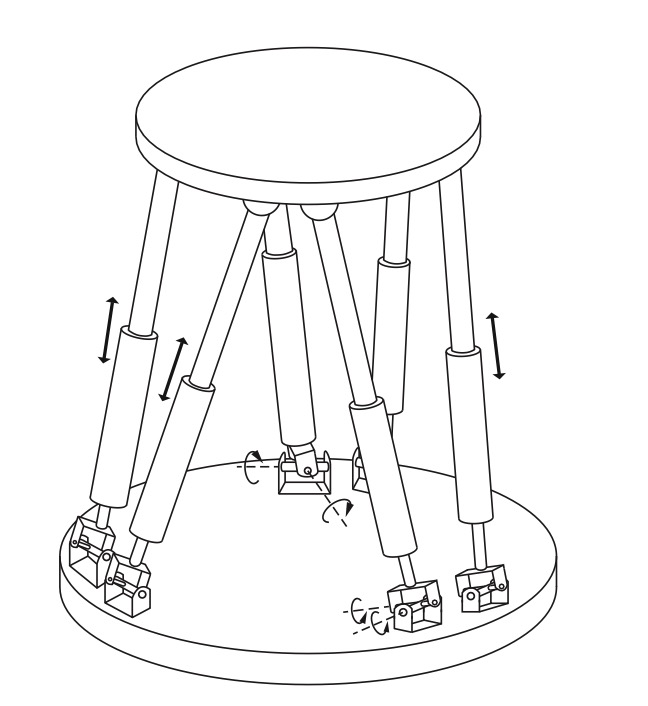
Fig. 16 Stewart-Gough platform

The Stewart-Gough platform consists of two platforms - the lower one stationary and regarded as ground, the upper one mobile - connected by six universal-prismatic-spherical (UPS) legs. The total number of links is \(14(N=14)\). There are six universal joints (each with two degrees of freedom, \(f_{i}=2\) ), six prismatic joints (each with a single degree of freedom, \(f_{i}=1\) ), and six spherical joints (each with three degrees of freedom, \(f_{i}=3\) ). The total number of joints is 18 . Substituting these values into Grübler’s formula with \(m=6\) yields

\[\operatorname{dof}=6(14-1-18)+6(1)+6(2)+6(3)=6 .\]

Configuration Space

Consider a point moving on the surface of a sphere. The C-space is 2-dimensional, as the configuration can be described by two coordinates: latitude and longitude. As another example, a point moving on a plane also has a two-dimensional C-space, with coordinates \((x, y)\). While both a plane and the surface of a sphere are 2-dimensional, they do not have the same shape. Unlike the plane, a larger sphere has the same shape as the original sphere, in that it wraps around in the same way. Only its size is different. For that matter, an oval-shaped American football also wraps around similarly to a sphere. The idea that the 2-dimensional surfaces of a small sphere, a large sphere, and a football all have the same kind of shape, which is different from the shape of a plane, is expressed by the topology of the surfaces. Two spaces are topologically equivalent if one can be continuously deformed into the other without cutting or gluing. A sphere can be deformed into a football simply by stretching, without cutting or gluing, so those two spaces are topologically equivalent. You cannot turn a sphere into a plane without cutting it, however, so a sphere and a plane are not topologically equivalent.

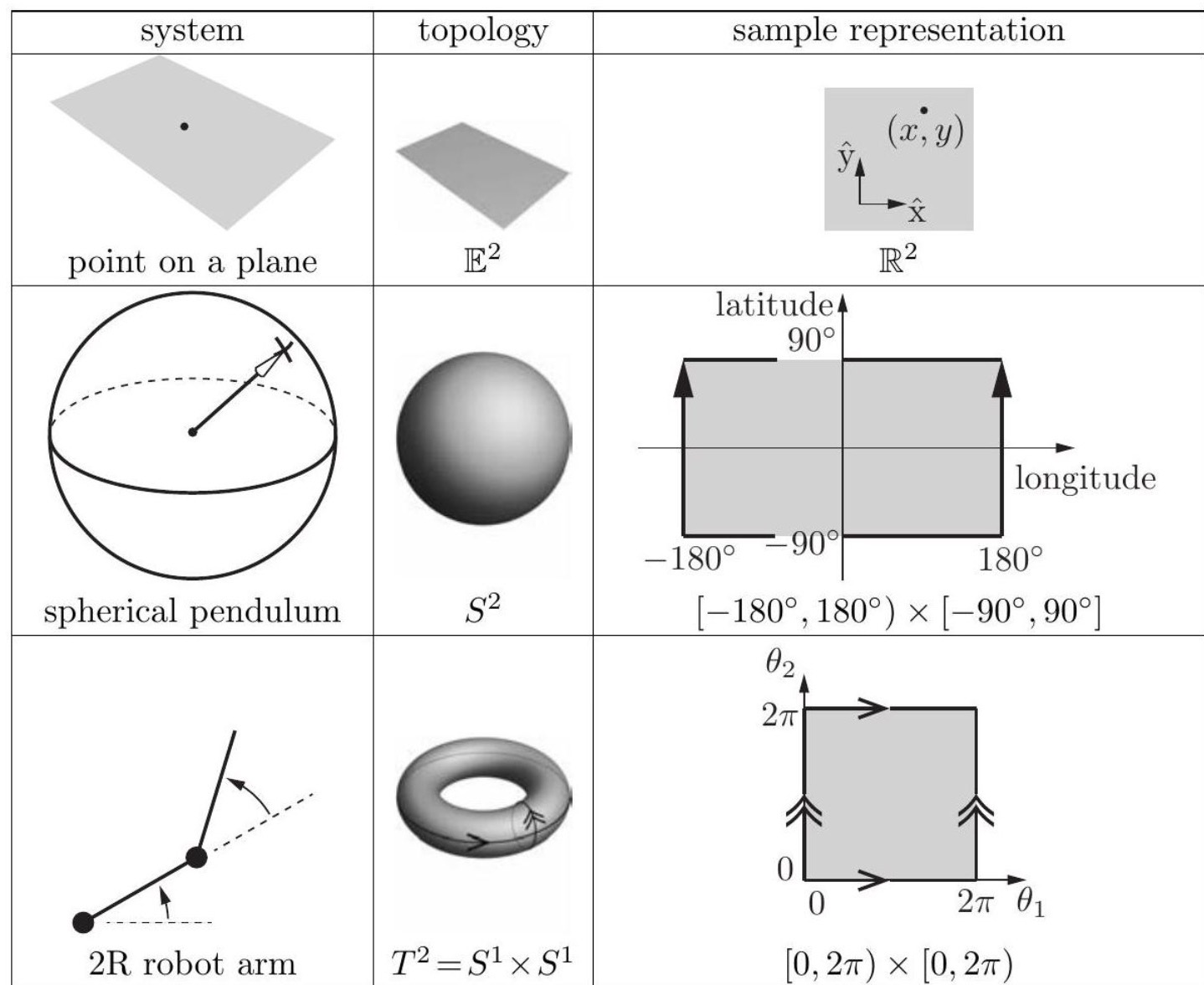
Fig. 17 Three topologically different two-dimensional C-spaces and coordinate representations. In the latitude-longitude representation of the sphere, the latitudes \(-90^{\circ}\) and \(90^{\circ}\) each correspond to a single point (the South Pole and the North Pole, respectively), and the longitude parameter wraps around at \(180^{\circ}\) and \(-180^{\circ}\); the edges with the arrows are glued together. Similarly, the coordinate representations of the torus wrap around at the edges marked with corresponding arrows.

There are two coordinate parameterizations/representations for a topology space.

• explicit parametrization: A choice of \(n\) coordinates, or parameters, to represent an \(n\)-dimensional space is called an explicit parametrization of the space. Such an explicit parametrization is valid for a particular range of the parameters (e.g., \(\left[-90^{\circ}, 90^{\circ}\right]\) for latitude and \(\left[-180^{\circ}, 180^{\circ}\right.\) ) for longitude for a sphere, where, on Earth, negative values correspond to “south” and “west,” respectively).

• implicit parametrization: An implicit representation views the \(n\)-dimensional space as embedded in a Euclidean space of more than \(n\) dimensions, just as a two-dimensional unit sphere can be viewed as a surface embedded in a three-dimensional Euclidean space. An implicit representation uses the coordinates of the higher-dimensional space (e.g., \((x, y, z)\) in the three-dimensional space), but subjects these coordinates to constraints that reduce the number of degrees of freedom (e.g., \(x^{2}+y^{2}+z^{2}=1\) for the unit sphere).

Workspace of Manipulators

The workspace is the portion of the environment the manipulator’s end-effector can access. Its shape and volume depend on the manipulator structure as well as on the presence of mechanical joint limits. Note that the workspace is independent of the task. In the following, we will show the workspace of different most common manipulators.

Cartesian manipulator includes three prismatic joints whose axes typically are mutually orthogonal.

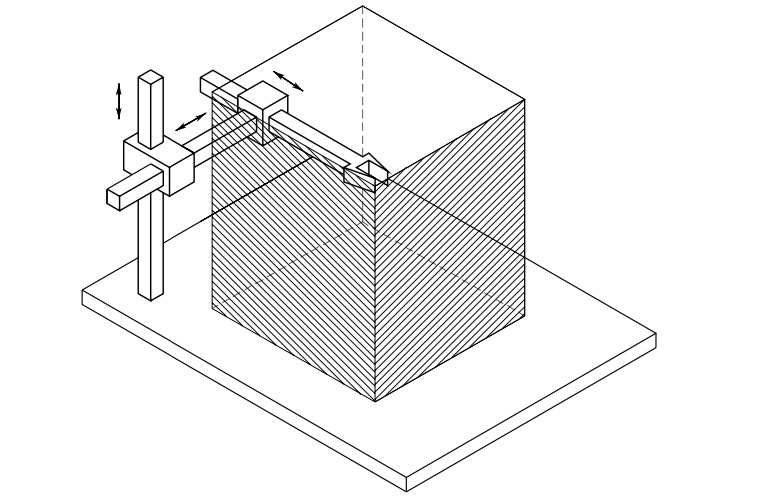
Fig. 18 Cartesian manipulator and its workspace

Cylindrical manipulator differs from Cartesian in that the first prismatic joint is replaced with a revolute joint.

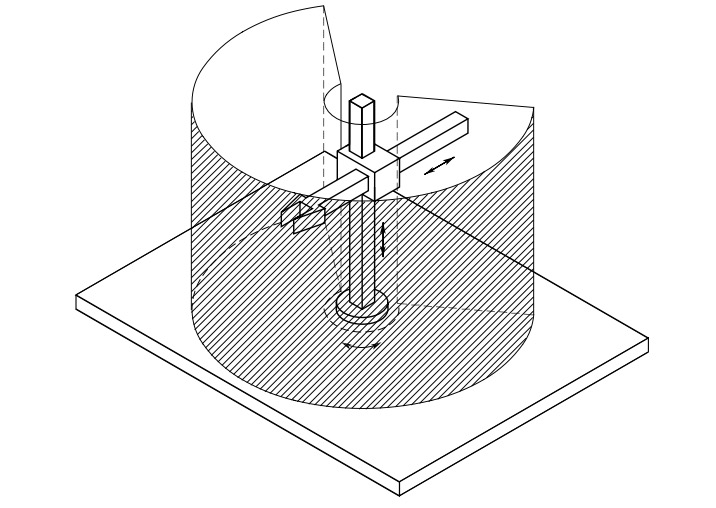
Fig. 19 Cylindrical manipulator and its workspace

Spherical manipulator differs from cylindrical in that the 2nd prismatic joint is replaced with a revolute joint.

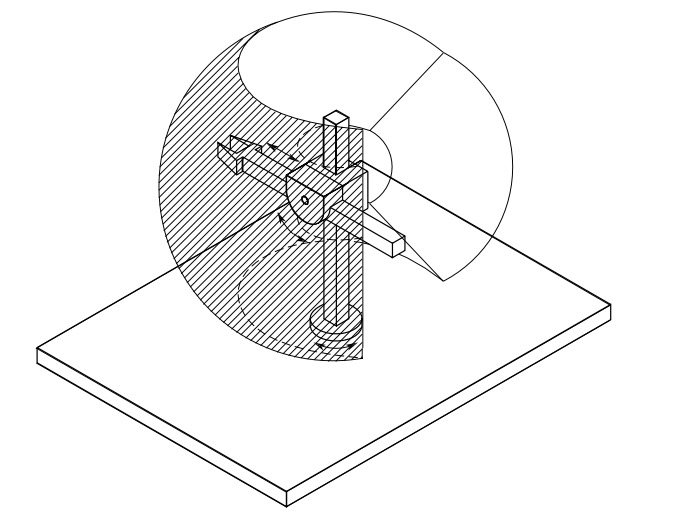
Fig. 20 Spherical manipulator and its workspace

A special manipulator is SCARA manipulator that can be realized by disposing two revolute joints and one prismatic joint in such a way that all the axes of motion are parallel.

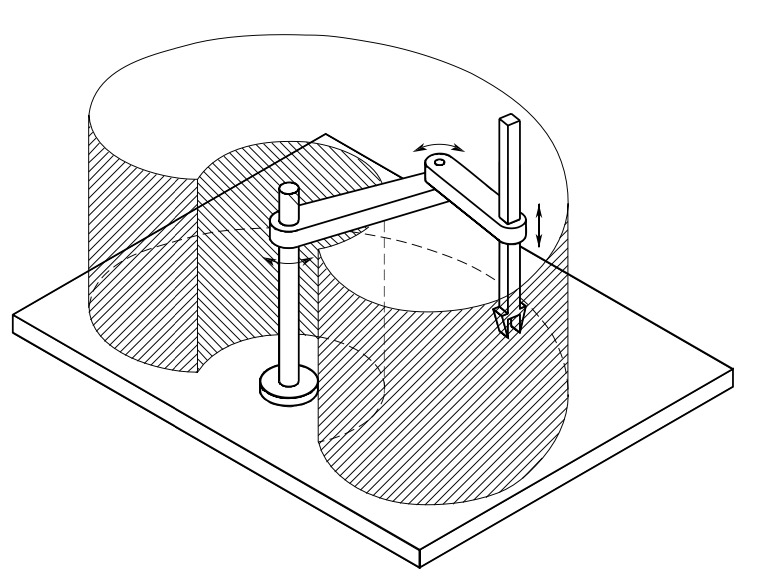
Fig. 21 SCARA manipulator and its workspace

Anthropomorphic manipulator is realized by three revolute joints; the revolute axis of the first joint is orthogonal to the axes of the other two which are parallel.

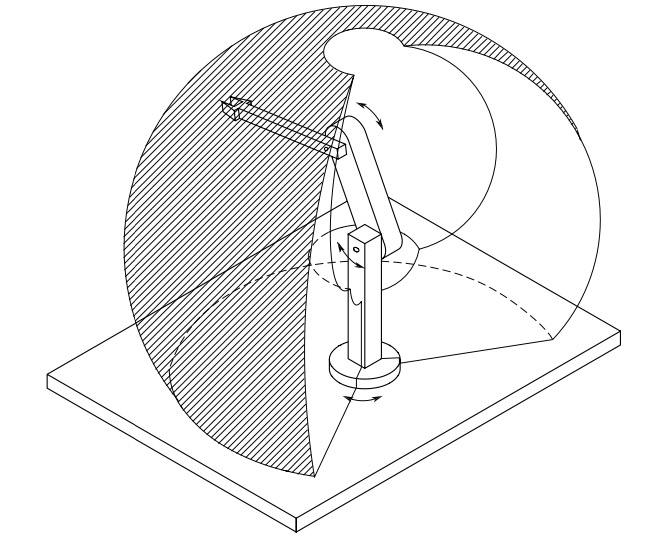
Fig. 22 Anthropomorphic manipulator and its workspace